
Viewing the least significant bit on top of single hexagrams in Shao Yong's square Īnd reading along rows either from bottom right to top left with solid lines as 0 and broken lines as 1 or from top left to bottom right with solid lines as 1 and broken lines as 0 hexagrams can be interpreted as sequence from 0 to 63. The Song Dynasty scholar Shao Yong (1011–1077) rearranged the hexagrams in a format that resembles modern binary numbers, although he did not intend his arrangement to be used mathematically. Eight trigrams (Bagua) and a set of 64 hexagrams ("sixty-four" gua), analogous to the three-bit and six-bit binary numerals, were in use at least as early as the Zhou Dynasty of ancient China. It is based on taoistic duality of yin and yang. The binary notation in the I Ching is used to interpret its quaternary divination technique. The I Ching dates from the 9th century BC in China. This method can be seen in use, for instance, in the Rhind Mathematical Papyrus, which dates to around 1650 BC. In this method, multiplying one number by a second is performed by a sequence of steps in which a value (initially the first of the two numbers) is either doubled or has the first number added back into it the order in which these steps are to be performed is given by the binary representation of the second number. The method used for ancient Egyptian multiplication is also closely related to binary numbers. Early forms of this system can be found in documents from the Fifth Dynasty of Egypt, approximately 2400 BC, and its fully developed hieroglyphic form dates to the Nineteenth Dynasty of Egypt, approximately 1200 BC. Horus-Eye fractions are a binary numbering system for fractional quantities of grain, liquids, or other measures, in which a fraction of a hekat is expressed as a sum of the binary fractions 1/2, 1/4, 1/8, 1/16, 1/32, and 1/64. The scribes of ancient Egypt used two different systems for their fractions, Egyptian fractions (not related to the binary number system) and Horus-Eye fractions (so called because many historians of mathematics believe that the symbols used for this system could be arranged to form the eye of Horus, although this has been disputed). See also: Ancient Egyptian mathematics Arithmetic values thought to have been represented by parts of the Eye of Horus Leibniz was specifically inspired by the Chinese I Ching. However, systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, and India. The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, Juan Caramuel y Lobkowitz, and Gottfried Leibniz.

Negative numbers are commonly represented in binary using two's complement.
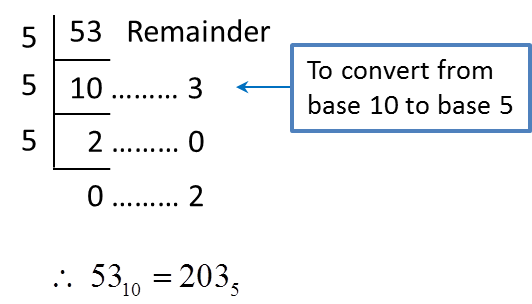
Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. Each digit is referred to as a bit, or binary digit. The base-2 numeral system is a positional notation with a radix of 2. A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method of mathematical expression which uses only two symbols: typically "0" ( zero) and "1" ( one).


 0 kommentar(er)
0 kommentar(er)
